Треугольник рело в круге

В современном мире, при быстро развивающихся технологиях нельзя обойти стороной фигуру постоянной ширины – треугольник Рёло, позволяющий сократить затраты при производстве, к примеру, при конструировании деталей.

Этой геометрической фигуре,ее применению и свойствам посвящена работа.

Просмотр содержимого документа
«Научно-исследовательская работа “Треугольник Рёло”»

«Богучарская средняя общеобразовательная школа № 1»

по теме: «Треугольник Рёло»

Автор: Пономарёва Валерия Витальевна, 9 «А» класс

Руководитель: Алабина Галина Юрьевна,

Нащёкина Ольга Владимировна

Понятие треугольника Рёло ……….……. …………………………….……. 4

Свойства треугольника Рёло………………………………. 6

5.1. Сверление квадратных отверстий…………………. ………………. 10

5.4. Грейферный механизм в кинопроектах…………………………….….12

6. Треугольник Рёло в искусстве…………………………………..………. …….13

6.1. Треугольник Рёло в архитектуре……………. ……………………….13

6.2. Изобретение велосипеда с треугольными колёсами…..……………. 13

6.3. Повозка с треугольными колёсами…………………………………….15

Иногда в основе любой ширины и толщины нужно сделать отверстие с идеальным квадратным сечением. А вы когда-нибудь задумывались над тем, как сверлят квадратные отверстия? Советов, как добиться максимальной точности при минимальных затратах, множество. Я задумалась над вопросом, а как бы с этой задачей справился математик и смог бы он сделать лучше. Ответ оказался положительным. Оказывается, существует еще один способ для вырезания квадратных отверстий, в реализации которого косвенно поучаствовал математик. Итак, квадратные отверстия можно сделать при помощи специального сверла, в сечение которого заложена форма треугольника Рёло. Меня заинтересовало не только само по себе данное изобретение, но и необычная геометрическая фигура – круглый треугольник. Я узнала, что он называется треугольником Рёло и посвятила свою работу изучению его свойств и областей применения. А заодно поставила задачу выяснить, как геометрия позволяет этому чуду катиться и иметь удивительно плавный ход.

Область исследования – математика.

Объект исследования– треугольник Рёло.

Предмет исследования – понятие треугольника Рёло, его свойства и практическое применение.

Привести достаточное количество примеров применения свойств треугольника Рёло.

Изучить главные свойства и узнать как можно больше о треугольнике Рёло.

На основе изученных материалов предложить области использования треугольника Рёло.

Познакомиться с историей изобретения.

Рассмотреть области применения фигур постоянной ширины.

2. Понятие треугольника Рёло.

Треугольник Рёло представляет собой область пересечения трёх равных кругов с центрами в вершинах правильного треугольника и радиусами, равными его стороне.

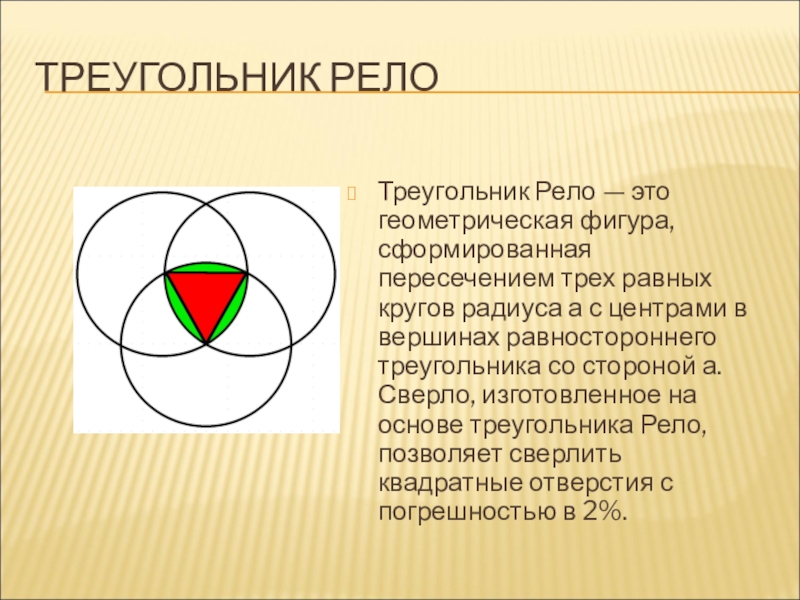
Построение треугольника Рёло циркулем

Треугольник Рёло можно построить с помощью одного только циркуля, не прибегая к линейке. Это построение сводится к последовательному проведению трёх равных окружностей. Центр первой выбирается произвольно, центром второй может быть любая точка первой окружности, а центром третьей — любая из двух точек пересечения первых двух окружностей.

3. Свойства треугольника Рёло.

Он обладает свойством кривых постоянной ширины.

Треугольник Рело – плоская фигура постоянной ширины — его можно вращать между двух параллельных прямых, расположенных на фиксированном расстоянии друг от друга, и он будет постоянно касаться их обеих. Добавим еще пару параллельных прямых, касающихся треугольника Рело и образующих с уже имеющимися прямой угол. Тем самым получим квадрат. Если вращать треугольник Рело специальным образом, то он будет постоянно находиться внутри квадрата и в любой момент касаться всех его сторон. Если быть более точным, то надо рассматривать квадрат с немного скругленными углами. При этом треугольник Рело является в этом «квадрате» ротором минимальной площади – той фигурой, которая при любом повороте будет касаться всех сторон, и при этом более маленькой по площади фигуры с таким условием не существует. Кроме окружности и треугольника Рело бывают и другие фигуры постоянной ширины. На любом правильном нечетном n–угольнике, так же как и на треугольнике, можно построить кривую постоянной ширины. Бывают несимметричные кривые постоянной ширины. Но бывает и бесконечно много фигур постоянной ширины, построенных именно на правильном треугольнике, и не подобных ни друг другу, ни треугольнику Рело.

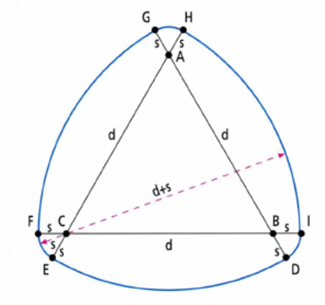
Теорема Барбье: Все кривые постоянной ширины h имеют одинаковую длину, равную πh.

Треугольника Рёло симметричен, обладает осевой симметрией. Он имеет три оси симметрии, каждая из которых проходит через вершину треугольника и середину противоположной стороны.

Поскольку треугольник Рёло является фигурой постоянной ширины, он обладает всеми общими свойствами фигур этого класса:

– с каждой из своих опорных (параллельных) прямых треугольник Рёло имеет лишь по одной общей точке;

– расстояние между двумя любыми точками треугольника Рёло не может превышать его ширины;

– отрезок, соединяющий точки касания двух параллельных опорных прямых к треугольнику Рёло, перпендикулярен к этим опорным прямым;

– через любую точку границы треугольника Рёло проходит по крайней мере одна опорная прямая;

– через каждую точку границы треугольника Рёло проходит объемлющая его окружность радиуса , причём опорная прямая, проведённая к треугольнику Рёло через точку , является касательной к этой окружности;

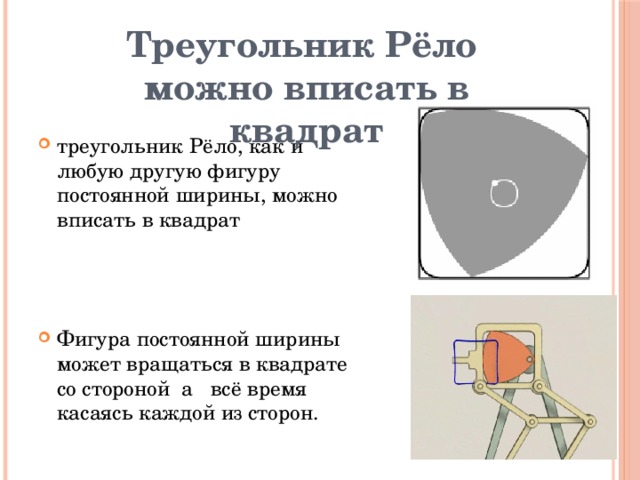
– треугольник Рёло, как и любую другую фигуру постоянной ширины, можно вписать в квадрат.

–Среди всех фигур постоянной ширины у треугольника Рёло наименьшая площадь. Чтобы найти площадь треугольника Рёло, можно сложить площадь внутреннего равностороннего треугольника и площадь трёх оставшихся одинаковых круговых сегментов, опирающихся на угол в 60°.

– Наименьший угол. Через каждую вершину треугольника Рёло, в отличие от остальных его граничных точек, проходит не одна опорная прямая, а бесконечное множество опорных прямых. Пересекаясь в вершине, они образуют «пучок». Угол между крайними прямыми этого «пучка» называется углом при вершине. Для фигур постоянной ширины угол при вершинах не может быть меньше 120°. Единственная фигура постоянной ширины, имеющая углы, равные в точности 120° — это треугольник Рёло.

По мнению историков, название это «непростой» простой фигуре дал немецкий механик Франц Рёло. Франц Рело родился 30 сентября 1829 г. в Эшвейлере, близ Ахена, в семье, для которой техника была традиционным занятием.Многие историки сходятся в том, что именно он стал первооткрывателем свойств этой геометрической фигуры. Потому как он первый широко использовал свойства и возможности треугольника Рёло в своих механизмах. Следовательно, изобретенный в прошлом веке треугольник Рёло широко используется сегодня. Однако его изучение не стоит на месте. Его свойства, как характеристики простой фигуры, находится в постоянном теоретическом и практическом изучении.

5. Практическое применение.

1. Сверление квадратных отверстий

Сверло с сечением в виде треугольника Рело и режущими кромками, совпадающими с его вершинами, позволяет получать почти квадратные отверстия. Отличие таких отверстий от квадрата состоит лишь в немного скруглённых углах. Другая особенность подобного сверла заключается в том, что его центр при вращении не остаётся на месте, как это происходит в случае традиционных спиральных свёрл, а описывает кривую, состоящую из четырёх дуг эллипсов. Поэтому патрон, в котором зажато сверло, не должен препятствовать этому движению.

Впервые сделать подобную конструкцию удалось Гарри Уаттсу, английскому инженеру, работавшему в США. Для сверления он использовалнаправляющий шаблон с квадратной прорезью, в котором двигалось сверло, вставленное в «плавающий патрон». Патенты на патрон и сверло были получены Уаттсом в 1917 году. Продажу новых дрелей осуществляла фирма WattsBrothersToolWorks. Ещё один патент США на похожее изобретение был выдан в 1978 году.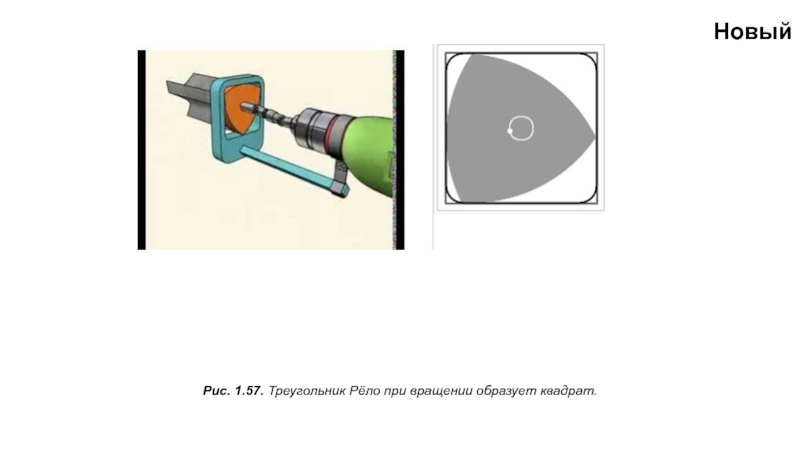

2. Двигатель Ванкеля

Другой пример использования можно найти в двигателе Ванкеля: ротор этого двигателя выполнен в виде треугольника Рёло. Он вращается внутри камеры, поверхность которой выполнена по эпитрохоиде. Вал ротора жёстко соединён с зубчатым колесом, которое сцеплено с неподвижной шестернёй. Такой трёхгранный ротор обкатывается вокруг шестерни, всё время касаясь вершинами внутренних стенок двигателя и образуя три области переменного объёма, каждая из которых по очереди является камерой сгорания. Благодаря этому двигатель выполняет три полных рабочих цикла за один оборот.

Двигатель Ванкеля позволяет осуществить любой четырёхтактный термодинамический цикл без применения механизма газораспределения. Смесеобразование, зажигание, смазка, охлаждение и пуск в нём принципиально такие же, как у обычных поршневых двигателей внутреннего сгорания.

Впервые на серийных автомобилях этот двигатель стала устанавливать компания Mazda. Он установлен на моделях MazdaRX-7 и MazdaRX-8.

3. Крышки для люков

В форме треугольника Рёло можно изготавливать крышки для люков — благодаря постоянной ширине они не могут провалиться в люк. В Сан-Франциско подобные крышки используются для системы рекуперированной воды.

4. Грейферный механизм в кинопроекторах

Также треугольник использовался в грейферном механизме в кинопроекторах. Двигатели дают равномерное вращение оси, а чтобы на экране было четкое изображение, пленку мимо объектива надо протянуть на один кадр, дать ей постоять, потом опять резко протянуть и так 18 раз в секунду. Именно эту задачу решает грейферный механизм. Он основан на треугольнике Рело, вписанном в квадрат и двойном параллелограмме, который не дает квадрату наклоняться в стороны.

Действительно, т.к. длины противоположных сторон равны, то среднее звено при всех движениях остается параллельным основанию, а сторона квадрата всегда параллельной среднему звену. Чем ближе ось крепления к вершине треугольника Рело, тем более близкую к квадрату фигуру описывает зубчик грейфера.

Читать также: Недостаток литья в оболочковые формы

Треугольник Рёло — распространённая форма плектра (медиатора): тонкой пластинки, предназначенной для приведения в состояние колебания струн щипковых музыкальных инструментов.

6. Треугольник Рёло в искусстве

1. Треугольник Рёло в архитектуре

Форма треугольника Рёло используется и в архитектурных целях. Окна в форме треугольника Рёло можно обнаружить в церкви Богоматери в Брюгге, а также в шотландской церкви в Аделаиде.

2. Изобретение велосипеда с треугольными колесами

1) Колесо, изобретенное несколько тысяч лет назад, произвело переворот в жизни человека. Постоянство ширины явилось для колеса определяющим свойством, следствием которого явилось техническое завоевание мира.«Изобретением велосипеда» называют бессмысленное повторение и переоткрытие давно пройденного и известного, и совершенно напрасно. Современные инженеры, можно сказать, постоянно изобретают велосипед, внося все новые усовершенствования в его конструкцию и отдельные детали. Однажды в интернете мы прочитали об одном удивительном изобретении китайского пенсионера – велосипеде с треугольными колесами.

Изобретением колес велосипеда занимается китайский рационализатор Гуань Байхуа, 50-летний офицер из города Циндао. Больше того, он изобретает заново самую консервативную деталь велосипеда – колеса. Вместо понятных всем круглых он предложил кататься на колесах пяти – и треугольной формы (спереди и сзади, соответственно). Для китайцев велосипед – главный вид транспорта, популярностью затмевающий автомобили. Но велосипед с угловатыми колесами средством передвижения не станет. По словам изобретателя, поездка на нем требует больше усилий, чем на обычном велосипеде, и скорее всего, он найдет свою нишу в качестве экзотической игрушки и более эффективного тренажера. Впрочем, все, кто пробовал прокатиться на нем, удивляются вовсе не трудности кручения педалей, а неожиданной плавности хода.
Действительно, казалось бы, угловатые колеса неизбежно должны создавать при качении существенную тряску – но ее Гуаню Байхуа удалось снизить благодаря прекрасному знанию геометрии и настоящей китайской хитрости.

2) Изготовление велосипеда с помощью 3D ручки

3. Повозка с «треугольными» колесами.

Для перемещения тяжёлых предметов на небольшие расстояния можно использовать не только колёсные, но и более простые конструкции, например, цилиндрические катки. Для этого груз нужно расположить на плоской подставке, установленной на катках, а затем толкать его. По мере освобождения задних катков их необходимо переносить и класть спереди. Такой способ транспортировки человечество использовало до изобретения колеса. При этом перемещении важно, чтобы груз не двигался вверх и вниз, так как тряска потребует дополнительных усилий от толкающего. Для того, чтобы движение по каткам было прямолинейным, их сечение должно представлять собой фигуру постоянной ширины. Чаще всего сечением был круг, ведь катками служили обыкновенные брёвна. Однако сечение в виде треугольника Рёло будет ничуть не хуже и позволит передвигать предметы столь же прямолинейно.

Таким же образом можно устроить подвеску некруглого колеса и взяв четыре таких подвески, можно соорудить повозку. При этом она будет ехать совершенно без покачиваний! Чтобы убедиться, что тряски нет, можно поставить, как учат автомобилистские традиции, на тележку стакан с водой.

Я попробовала соорудить такую повозку и опытным путем проверить гипотезу об отсутствии качки.

ПРИМЕНЕНИЕ ТРЕУГОЛЬНИКА РЁЛО

класс 11 «Б», МОУ гимназия № 11, г. Волгоград

Резниченко Дарья Анатольевна

научный руководитель, учитель первой категории, учитель математики и информатики, МОУ гимназия № 11, г. Волгоград

Актуальность: в современном мире, при быстро развивающихся технологиях нельзя обойти стороной фигуру постоянной ширины — треугольник Рёло, позволяющий сократить затраты при производстве, к примеру, при конструировании деталей.

Объектом исследования является треугольник Рёло.

Цель исследования: привести достаточное количество примеров применения свойств треугольника Рёло.

Для решения поставленной цели были выделены следующие задачи исследования:

·изучить главные свойства треугольника Рёло;

·отсмотреть видео материал про треугольник Рёло;

·на основе изученных материалов предложить области использования треугольника Рёло.

Методами исследования являются изучение документации и информационных материалов, наблюдение, анализ, эксперимент.

Как и большинству подростков старшего школьного возраста поколения 90-х, меня интересуют спортивные автомобили. Особое внимание я уделяю эксклюзивным моделям. Поэтому сильно привлекает моё внимание машина Mazda RX-7 и чуть позже RX-8, где интерес вызывает двигатель этих машин. Речь идет о «двигателе Ванкеля», или о «роторном двигателе».

В свое время Ванкель сделал прорыв в машинной индустрии, создав двигатель кардинально отличавшиеся от поршневого. Главным отличаем является количество движущихся частей, такой главной деталью в двигателе будет ротор. Только благодаря особой форме ротора такой двигатель возможен. Эта форма носит название — «Треугольник Рёло», или в простонародье круглый треугольник (Рис.1). Фигура «треугольник Рёло» меня заинтересовала, и я решил разобраться в её свойствах и способах применения.

Я начал с того, что решил изучить все свойства фигуры. И остановиться на тех, которые помогут понять, куда её можно применить. Первое — её построение. Такую фигуру очень просто построить, используя только циркуль. Для этого нужно провести две окружности с одинаковым радиусом, но так, чтобы центр второй совпадал с одной из точек первой (кроме центра). Проводим третью окружность, так что бы её центр совпадал с точкой пересечения первых окружностей (Рис. 1). Область, которая принадлежит всем трем кругам и есть треугольник Рёло.

Треугольник Рёло, является фигурой постоянной ширины. Это означает, что если провести две параллельные прямые на некотором расстоянии, то фигура при качении будет касаться обеих прямых постоянно. Расстояние между ними и будет фигура постоянной ширины. Простейшей такой фигурой будет всем известный круг. На самом деле таких фигур не мало. Среди ряда таких фигур наименьшая площадь у треугольника Рёло. Это утверждение носит название теоремы Бляшке — Лебега. К примеру, если его вписать в круг, то разница очевидна (Рис. 2).

Пусть а — это ширина фигуры, тогда площадь , а периметр (Рис. 3).

Рисунок 3. Треугольник Рёло

Треугольник Рёло обладает тремя осевыми линиями, которые проходят из вершины в середину противоположной стороны b.

Являясь фигурой постоянной ширины, треугольник Рёло обладает всеми общими свойствами фигур этого класса. А именно:

·с каждой из своих опорных прямых, треугольник Рёло имеет лишь по одной общей точке;

·расстояние между двумя любыми точками треугольника Рёло ширины не может превышать а;

·отрезок, соединяющий точки касания двух параллельных опорных прямых к треугольнику Рёло, перпендикулярен к этим опорным прямым;

·через любую точку границы треугольника Рёло проходит, по крайней мере, одна опорная прямая;

·через каждую точку границы треугольника Рёло проходит объемлющая его окружность радиуса, причём опорная прямая, проведённая к треугольнику Рёло через точку, является касательной к этой окружности;

·радиус окружности, имеющей не меньше трёх общих точек с границей треугольника Рёло ширины, не превышает;

·по теореме Ханфрида-Ленца о множествах постоянной ширины треугольник Рёло нельзя разделить на две фигуры, диаметр которых был бы меньше ширины самого треугольника;

·треугольник Рёло, как и любую другую фигуру постоянной ширины, можно вписать в квадрат, а также в правильный шестиугольник;

·по теореме Барбье формула периметра треугольника Рёло справедлива для всех фигур постоянной ширины.

Не опровержим тот факт, что свойство треугольника Рёло — качение по квадрату, позволяет применять его в интересных областях (Рис. 4).

Рисунок 4. Качение по квадрату

Треугольник Рёло вписан в квадрат и может вращаться в нём, постоянно касаясь всех четырёх сторон. Каждая вершина треугольника при его вращении «проходит» почти весь периметр квадрата, отклоняясь от этой траектории лишь в углах — там вершина описывает дугу эллипса. Центр этого эллипса расположен в противоположном углу квадрата, а его большая и малая оси повёрнуты на угол в 45° относительно сторон квадрата и равны (Рис.4). Все 4 эллипса касаются смежных сторон квадрата на расстоянии от угла (Рис.5).

Изучив научную и справочную литературу по треугольнику Рёло, я выделил 4 области применения фигуры постоянной ширины.

Рисунок 6. Двигатель Ванкеля

Во-первых, это двигатель Ванкеля (Рис. 6), который возможен благодаря форме ротора. Он вращается внутри камеры, поверхность которой выполнена по эпитрохоиде[1]. Вал ротора жёстко соединён с зубчатым колесом, которое сцеплено с неподвижной шестерёнкой. Такой трёхгранный ротор обкатывается вокруг шестерни, касаясь вершинами внутренних стенок двигателя и образуя три области переменного объёма, каждая из которых по очереди является камерой сгорания. Благодаря этому двигатель выполняет три полных рабочих цикла за один оборот.

Во-вторых, кинематография, а более точно — «Грейферный» механизм (Рис. 7), который осуществляет покадровое перемещение плёнки в кинопроекторах. В данном случае треугольник Рёло находится внутри квадрата и двигает рамку, посредством вращения вокруг одного из своих углов. Зуб, который находиться на рамке, входит в перфорацию киноплёнки, протаскивает её на один кадр вниз и выходит обратно.

Рисунок 7. Грейферный механизм

В-третьих, с помощью сверла формы треугольника Рёло можно сверлить квадратные отверстия! Замечено что вершины треугольника Рёло описывают квадрат только при вращение центра строго по фигуре состоящей из 4 дуг эллипсов (Рис.4). Отсюда и сложность создания такого сверла, так как обычная дрель вращает сверло вокруг своей оси. Но все-таки, конструкция позволяющая воплотить такое сверло, было придумано Гарри Уаттсу в 1917 году (Рис. 8).

Читать также: Как развальцевать железную тормозную трубку

Рисунок 8. Сверло Уаттсу

В-четвертых, это медиатор музыкантов-струнников, а так же диаграммы Эйлера RGB.

Основываясь на теоретических данных, предполагаю, что свойства треугольника Рёло возможно использовать в следующих направлениях:

1. Создание и использование машины для дробления камней в шахтах. Для этого необходимо изготовить два вала, которые при фронтальном срезе будут в форме треугольника Рёло, причем вершины треугольника имеют зубья, глубина которых равна разнице расстояния от центра до вершины, и расстоянию от центра до самой удаленной точки на стороне (Рис. 9).

Рисунок 9. Вал дробильной машины (вид сбоку)

Которые надо расположить таким образом, что их оси будут находиться на расстоянии, равном двум расстояниям от самой удаленной точки стороны треугольника (назовем её х) до его центра, плюс 15 % от этого расстояния, и начать их вращать. При вращение мы будем наблюдать две фазы. Первая, когда точки х обоих валов будут на не большом (15 %) расстоянии друг от друга (Рис.10), и вторая, когда зубчатые вершины треугольника Рёло будут входить друг в друга с небольшим зазором (Рис. 11).

Рисунок 10. Первая фаза

Рисунок 11. Вторая фаза

В первой фазе камни будут попадать в зазор, а во второй дробиться. Причем, если по той же технологии расположить круглые валы, то вероятность того, что конструкция заклинит выше, потому что при вращение круглых валов, всего одна фаза, при которой камни и попадают в дробильный механизм, и дробятся одновременно. В случае с машиной, в которой применен треугольник Рёло, фазы две, и даже, если при дроблении камень застрял, то в следующей фазе механизм образует зазор, и машина не застопорится. К тому же, современная дробилка устроена таким образом, что в ней присутствует возвратнопоступательный механизм. На примере сравнения двигателя Ванкеля и поршневого двигателя (и здесь можно выделять те же плюсы).

2. Тренажеры для развития различных групп мышц. Главная цель современных тренажеров, это изолированная тренировка мышцы. Но время не стоит на месте и биомеханика, позволила понять, что важно не только изолировать мышцу, но и правильно давать на нее нагрузку. Так как мышца не способна одинаково сильно работать на протяжении всего своего «рабочего хода», то надо давать слабую нагрузку в момент, когда она находиться в одном из крайних положений и когда она проходит «центральное» положение, нагрузка может возрастать. Но такого эффекта сложно добиться, для этого используют различные кулачковоблочные механизмы, и такие тренажеры отличаются дороговизной. В свою очередь использования треугольника Рёло для этой цели очень эффективно заменяет все сложные механизмы. Работая пятое лето подряд у отца на заводе по изготовлению тренажеров, и занимаясь последние два лета непосредственно разработкой такого вида тренажеров, как никто другой, я знаю, как сложно создать такой механизм. И вот теперь я произвел расчеты, что, если тянуть трос не через кулачковоблочный механизм, а через блок в виде треугольника Рёло, то экономиться приблизительно 2 метра троса который проходит через такую систему, и сокращается расход метала. А результат изменения нагрузки будет таким же, нагрузка будет с начало возрастать, а затем она станет пиковой в момент прохождения вершины треугольника Рёло, а затем снова сходить на нет, при условии, что мы тянули один и тот же вес. Нагрузка на мышцу получилась плавная и равномерная.

3. Люки канализации. Фигура постоянной ширины не может проходить через отверстие такой же фигуры с меньшей шириной. Благодаря чему можно треугольник Рёло использовать и в этом направление тоже. Тут, конечно, можно рассуждать, что и круглый люк не проваливается, так как круг тоже фигура постоянной величины, но нам уже известен тот факт, что у треугольника Рёло меньше площадь, чем у круга, а значит и материала меньше расходуется на крышку люка. Это придумал не я. Но я думаю это актуально и сейчас.

4. Музыкальные инструменты. Я окончил музыкальную школу по классу баян. Поэтому знаю, какие минусы есть у моего инструмента. Один из них это, что при нажатии на клавиши близко стоящие во 2 и 3 ряду они цепляют друг за друга в виду небольшого смешения, что не приемлемо. Если же клавиши сделать в форме треугольника Рёло, и расположить их, как показано на рисунке 12, то такой проблемы можно избежать. Причем инструмент будет более экстравагантный.

Рисунок 12.Клавиши баяна

5. Также нашел применение треугольника Рёло в мотоиндустрии. Сам я, с недавних пор, увлекся мотоциклами, и, соответственно, туда тоже применил эту фигуру. Всем известно, для того, чтобы приводить мотоцикл в движение необходимо «крутить ручку газа». В мотоиндустрии проблема с хорошим хватом этой ручки стоит остро. Её решали по-разному, к примеру: используя материалы, повышающие трение между перчаткой и грипсой (ручкой газа). К тому же, при длительной езде рука попросту устает. Ради решения моей проблемы, я изготовил из дерева ручку, которая при фронтальном разрезе имела форму треугольника Рёло и, как оказалось, она идеально повторяет внутренние контуры закрытой ладони, и удерживать такую рукоять гораздо легче. Как оказалось, при простейшем изучении вашей ладони вы увидите, что если собрать руку «трубочкой», как будто вы держите что-нибудь круглое, то вторая и третья фаланга второго, третьего и четвертого, а также вторая фаланга первого пальца (замыкающего «кольцо» из вашей ладони) образуют вершины круглого треугольника, что полностью доказывает мою гипотезу. Данное открытие можно использовать не только для ручек мотоцикла, но и везде где необходимо удерживать с сопротивлением поворотную рукоять такого типа.

На самом деле, треугольник Рёло называется так не по праву. Потому что сам Рёло, только описал и изучил круглый треугольник, но никак не придумал его. Это легко проверить, заглянув в работы Леонардо-де Винчи. Еще можно встретить эту фигуру в архитектуре ранее.

Что же я получили в ходе работы? Изучив литературу, просмотрев видео материалы, рассмотрев большое количество областей, которые укладываются в мой кругозор, где только возможно применение треугольника Рёло, мы получили интересный результат. А заключается он в том, что применение данного треугольника в окружающем нас мире, может быть гораздо большем, чем мы могли бы подумать. Я считаю, что нельзя так беззаботно обходить треугольник Рёло, его можно использовать в различных механизмах. Это подобно великому русскому языку. Ведь столько слов, которые мы можем использовать, не заимствуя их с других языков. Не применяя русские слова, мы используем иностранные. Так, не учитывая во внимание существование данной фигуры, мы стараемся изобрести что-то новое. А так ли это необходимо? Не всегда. Иногда необходимо лишь углубить свои знания в той или иной области. И ответ окажется очень простым. Знание о треугольнике Рёло, действительно облегчает нашу жизнь.

1.Радемахер Г., Тёплиц О. Кривые постоянной ширины // Числа и фигуры. Опыты математического мышления / Пер. с нем. В.И. Контовта. — М.: Физматгиз, 1962. — С. 195—211. — 263 с. — («Библиотека математического кружка», выпуск 10). [Электронный ресурс] — Режим доступа. — URL: http://ru.wikipedia.org/wiki/Треугольник_Рёло (дата обращения 22.04.13).

[1] Эпитрохоида — (греч. trochoeidеs — колёсообразный, круглый, от trochоs — колесо, круг и еidos — вид), плоская кривая, описываемая точкой, неизменно связанной с окружностью (или прямой), катящейся без скольжения по другой окружности или прямой. — Большая энциклопедия.

1. Введение 3 стр.

2. Основная часть 5 стр.

3. Эксперимент 9 стр.

4. Заключение 11 стр.

5. Литература 12 стр.

6. Приложения 13 стр.

Введение

Проблема: При изучении темы «треугольники» уроках геометрии я узнал, что среди них можно выделить: равнобедренные ,равносторонние, прямоугольные.

Однако, посмотрев телепередачу «Галилео», я с удивлением обнаружил существование «круглого» треугольника

Для того, чтобы выяснить, знают ли ученики нашей школы о «круглом» треугольнике, aмною был проведен опрос. Было опрошено 70 учащихся 7-11 классов. (Анкета. Приложение 1.)Опрос показал, что два человека имеют представление о треугольнике, а желают узнать о таком треугольнике почти 92% опрошенных. Таким образом, понятно, что учащиеся желают узнать для себя новый материал, который не изучается в школьной программе.

Фигура треугольника Рёло меня заинтересовала, и я решил разобраться в его свойствах и способах применения.

Актуальность:

Исторически геометрия начиналась с треугольника, поэтому треугольник не только символ геометрии, но и атом геометрии. Постоянно открываются все новые и новые свойства треугольника. Чтобы рассказать обо всех известных его свойствах, потребуется том величиной в несколько тысяч страниц.

Геометрия треугольника дает возможность почувствовать красоту математики вообще и может стать для кого-то началом пути в «большую науку». Каждый любитель геометрии треугольника имеет возможность открыть нечто новое и пополнить её сокровищницу собственной драгоценной находкой, ибо геометрия поистине неисчерпаема.

В современном мире при быстро развивающихся технологиях нельзя обойти фигуру постоянной ширины – треугольника Рёло, позволяющего сократить затраты при производстве, к примеру, при конструировании деталей.

Читать также: Как обрезать зеркало болгаркой

Практическая значимость моего исследования заключается в том, что удивительные свойства треугольника Рёло позволяют сделать новые открытия в разных областях жизнедеятельности человека: механике, искусстве и др.

Объект исследования: треугольник Рёло

Предмет исследования: практическое применение свойствтреугольника Рёло.

Цель: доказать, чтогеометрия необходима в практической жизни, знание этой науки раскрывает возможности деятельности человека.

Задачи:

1. Узнать, что такое треугольник Рёло?

2. Выделить его основные свойства.

3. Определить, где встречается треугольник Рёло, применение его свойств.

Гипотеза: У треугольника Рёло есть свои уникальные свойства, которые могут использоваться в разных областях жизнедеятельности человека.

Методы работы: изучение научной литературы, опрос, наблюдение, анализ, эксперимент.

Основная часть.

Изучив научную литературу в Интернет-ресурсе, я узнал, что название фигуры происходит от фамилии немецкого механика Франца Рёло (1829 – 1905) Наверное, именно он был первым, кто исследовал свойства этого треугольника; и использовал его в своих механизмах. В 1852 г. он окончил политехникум в Карлсруэ, с 1856г. был профессором Политехнического института в Цюрихе, а в 1864—1896 г. профессором Промышленного института (позже — Высшая техническая школа) в Берлине. В 1875 г. Франц Рёло впервые четко дал определение кинематической пары, кинематической цепи и механизма как кинематической цепи принуждённого движения; предложил способ преобразования механизмов путём изменения стойки и путём изменения конструкций кинематических пар. Впервые поставил и пытался решить проблему эстетичности красоты технических объектов, поэтому, современники Рёло называли его поэтом в технике. Творчество Рёло оказало значительное влияние на последующие исследования по теории механизмов. (Приложение 2)

Рёло не является первооткрывателем этой фигуры, хотя он и подробно исследовал её. Но он рассматривал вопрос о том, сколько контактов (в кинематических парах) необходимо, чтобы предотвратить движение плоской фигуры, и на примере искривлённого треугольника, вписанного в квадрат, показал, что даже трёх контактов может быть недостаточно для того, чтобы фигура не вращалась.

Некоторые математики считают, что первым продемонстрировал идею треугольника из равных дуг окружности Леонард Эйлер в XVIII веке.

Хотя эта фигура встречается и раньше, в XV веке: её использовал в своих рукописях Леонардо да Винчи. Треугольник Рёло есть в его манускриптах A и B, хранящихся в Институте Франции, а также в Мадридском кодексе.

Итак, что же такое «круглый» треугольник?

Треугольник Рёло представляет собой область пересечения трех равных кругов с центрами в вершинах правильного треугольника и радиусами, равными его стороне. Его можно построить с помощью одного только циркуля, не прибегая к линейке. Это построение сводиться к последовательному проведению трех равных окружностей. Нужно провести две окружности с одинаковым радиусом, но так, чтобы центр второй совпадал с одной из точек первой (кроме центра). Проводим третью окружность, так что бы её центр совпадал с точкой пересечения первых окружностей (Приложение 3). Область, которая принадлежит всем трем кругам и есть треугольник Рёло.

Каковы же свойства этой фигуры?

Треугольник Рёло, является фигурой постоянной ширины. Это значит, что если провести две параллельные прямые на некотором расстоянии, то фигура при качении (когда фигура будет катиться) будет касаться обеих прямых постоянно. Расстояние между ними и будет фигура постоянной ширины. Простейшей такой фигурой будет всем известный круг, хотя таких фигур немало. Среди этих фигур наименьшая площадь именно у треугольника Рёло. Это утверждение носит название теоремы Бляшке — Лебега. (по фамилиям немецкого геометра Вильгельма Бляшке и французского математика Анри Лебега) К примеру, если его вписать в круг, то разница очевидна (Приложение 4). Площадь соответствующего треугольника Рёло меньше на ≈ 10,27%

Треугольник Рёло является плоскойвыпуклойгеометрической фигурой.

Через каждую вершину треугольника Рёло, в отличие от остальных его граничных точек, проходит не одна опорная прямая, а бесконечное множество опорных прямых. Пересекаясь в вершине, они образуют «пучок». Угол между крайними прямыми этого «пучка» называется углом при вершине. Для фигур постоянной ширины угол при вершинах не может быть меньше 120°. Единственная фигура постоянной ширины, имеющая углы, равные в точности 120° — это треугольник Рёло.

Любую фигуру постоянной ширины можно вписать вквадрат со стороной, равной ширине фигуры, причём направление сторон квадрата может быть выбрано произвольно. Треугольник Рёло — не исключение, он вписан в квадрат и может вращаться в нём, постоянно касаясь всех четырёх сторон. (Приложение 5)

Каждая вершина треугольника при его вращении «проходит» почти весь периметр квадрата, отклоняясь от этой траектории лишь в углах.

Этими свойствами обусловлено практическое применение треугольника Рёло. Разница с площадью квадрата составляет ≈1,2 %, поэтому на основе треугольника Рёло создаютсвёрла, позволяющие получать у треугольника почти квадратные отверстия. Отличие таких отверстий от квадрата состоит лишь в немного скруглённых углах. Другая особенность подобного сверла заключается в том, что его центр при вращении не остаётся на месте, как это происходит в случае традиционных спиральных свёрл, а описывает кривую, состоящую из четырёх дуг эллипсов. Поэтому патрон, в котором зажато сверло, не должен препятствовать этому движению.(Приложение 6)

Впервые сделать подобную конструкцию удалось Гарри Уаттсу, английскому инженеру, работавшему в США.

Треугольник Рёло используется и в автомобильных двигателях. Их называют роторно-поршневыми. Первым такой двигатель создал в 1957 г. немецкий инженер Ф. Ванкель. Ротор этого двигателя выполнен в виде треугольника Рёло. Он вращается внутри камеры. Вал ротора жёстко соединён с зубчатым колесом, которое сцеплено с неподвижной шестернёй. Такой трёхгранный ротор обкатывается вокруг шестерни, всё время касаясь вершинами внутренних стенок двигателя и образуя три области переменного объёма, каждая из которых по очереди является камерой сгорания. Благодаря этому двигатель выполняет три полных рабочих цикла за один оборот.(Приложение 7)

Треугольник использовался в грейферном механизме в кинопроекторах. Двигатели дают равномерное вращение оси, а чтобы на экране было четкое изображение, пленку мимо объектива надо протянуть на один кадр, дать ей постоять, потом опять резко протянуть и так 18 раз в секунду. Именно эту задачу решает грейферный механизм.(Приложение 8,9 )

Треугольник Рёло широко применяется в кулачковых механизмах швейных машин зигзагообразной строчки.

В качестве кулачка треугольник Рёло использовали немецкие часовые мастера в механизме наручных часов A. Lange & Söhne «Lange 31»

Треугольник Рёло – распространённая форма медиатора– тонкой пластинки, предназначенной для приведения в состояние колебания струн щипковых музыкальных инструментов.

В форме треугольника Рёло можно изготавливатькрышки для люков— благодаря постоянной ширине они не могут провалиться в люк(так же люки использовались и в Сан — Франциско).(Приложение 10 )

В 1514 г. Леонардо да Винчи создал одну из первых в своём роде карт мира. Поверхность земного шара на ней была разделена экватором и двумя меридианами (угол между плоскостями этих меридианов равен 90°) на восемь сферических треугольников, которые были показаны на плоскости карты треугольниками Рёло, собранными по четыре вокруг полюсов. (Приложение 11)

Форма треугольника Рёло используется и в архитектурных целях. Конструкция из двух его дуг образует характерную для готического стиля стрельчатую арку, однако целиком он встречается в готических сооружениях довольно редко. Окна в форме треугольника Рёло можно обнаружить в церкви Богоматери в Брюгге, а так же в шотландской церкви в Аделаиде. Как элемент орнамента он встречается на оконных решетках аббатства в швейцарской коммуне Отрив.

Треугольник Рёло используют и в архитектуре, не принадлежащей к готическому стилю. Например, построенная в 2006 году в Кёльне 103-метровая башня под названием «Кёльнский треугольник» в сечении представляет собой именно эту фигуру. (Приложение 12,13,14)

Треугольник Рёло используется в изготовлении монет . Так уже не один, а несколько, объединенных в семиугольник.

Среди всех многоугольников Рёло с фиксированным числом сторон и одинаковой шириной правильные многоугольники ограничивают наибольшую площадь.

Форма таких многоугольников используется в монетном деле: монеты ряда стран. Например, монет 20 и 50 пенсов Великобритании выполнены в виде правильного семиугольника Рёло. Существует изготовленный китайским офицером велосипед, колёса которого имеют форму правильных треугольника и пятиугольника Рёло. (Приложение 15)

В научно-фантастическом рассказе Пола Андерсона «Треугольное колесо» экипаж землян совершил аварийную посадку на планете, население которой не использовало колёса, так как всё круглое находилось под религиозным запретом. В сотнях километров от места посадки предыдущая земная экспедиция оставила склад с запасными частями, но перенести оттуда необходимый для корабля двухтонный атомный генератор без каких-либо механизмов было невозможно. В итоге землянам удалось соблюсти табу и перевезти генератор, используя катки с сечением в виде треугольника Рёло.

Эксперимент

Тема: «Изготовление катка с сечением в виде треугольника Рёло»

Цель: исследование практического выполнения и применения свойств треугольника Рёло на примере катка; может ли треугольник Рёло быть круглым и использоваться для перемещения грузов

No related posts.

Мой Инструмент